Basic Optimization
[1]:
import sys
import os
sys.path.insert(0, os.path.abspath("."))
sys.path.append(os.path.abspath("../../../"))
This tutorial demonstrates how to perform optimization with DESC. It will go through two examples:
targeting the “triple product” quasi-symmetry objective \(f_T\) in the full plasma volume
targeting the “two-term” objective \(f_C\) for quasi-helical symmetry at the plasma boundary surface
These examples are adapted from a problem first presented in Rodriguez et al. (2022) and reproduced in Dudt et al. (2023).
If you have access to a GPU, uncomment the following two lines. You should see about an order of magnitude speed improvement with only these two lines of code!
[2]:
# from desc import set_device
# set_device("gpu")
[3]:
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams["font.size"] = 20
import desc.io
from desc.grid import LinearGrid, ConcentricGrid
from desc.objectives import (
ObjectiveFunction,
FixBoundaryR,
FixBoundaryZ,
FixPressure,
FixIota,
FixPsi,
AspectRatio,
ForceBalance,
QuasisymmetryBoozer,
QuasisymmetryTwoTerm,
QuasisymmetryTripleProduct,
)
from desc.optimize import Optimizer
from desc.plotting import (
plot_grid,
plot_boozer_modes,
plot_boozer_surface,
plot_qs_error,
plot_boundaries,
plot_boundary,
)
DESC version 0.10.2+349.g81f43916.dirty,using JAX backend, jax version=0.4.13, jaxlib version=0.4.13, dtype=float64
Using device: CPU, with 5.76 GB available memory
Initial guess
To save time during this tutorial, we will load an equilibrium solution to use as the initial guess for optimization. This equilibrium is already somewhat close to quasi-helical symmetry (QH) but can be improved.
[4]:
# load initial equilibrium
eq_init = desc.io.load("qs_initial_guess.h5")
[5]:
plot_boundary(eq_init, figsize=(8, 8))
[5]:
(<Figure size 768x768 with 1 Axes>,
<Axes: xlabel='$R ~(\\mathrm{m})$', ylabel='$Z ~(\\mathrm{m})$'>)
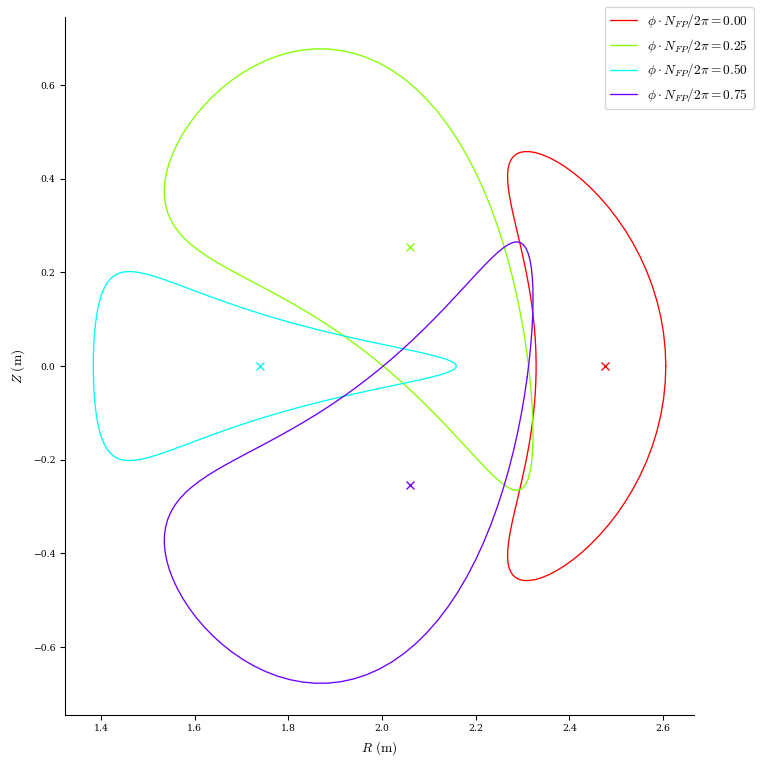
There are several plotting functions available in DESC that are useful for visualizing the quasi-symmetry (QS) errors. Let us look at the initial errors before optimization:
[6]:
# plot modes of |B| in Boozer coordinates
plot_boozer_modes(eq_init, num_modes=8, rho=10)
# plot |B| contours in Boozer coordinates on a surface (default is rho=1)
plot_boozer_surface(eq_init)
# plot normalized QS metrics
plot_qs_error(eq_init, helicity=(1, eq_init.NFP), rho=10)
[6]:
(<Figure size 576x576 with 1 Axes>, <Axes: xlabel='$\\rho$'>)
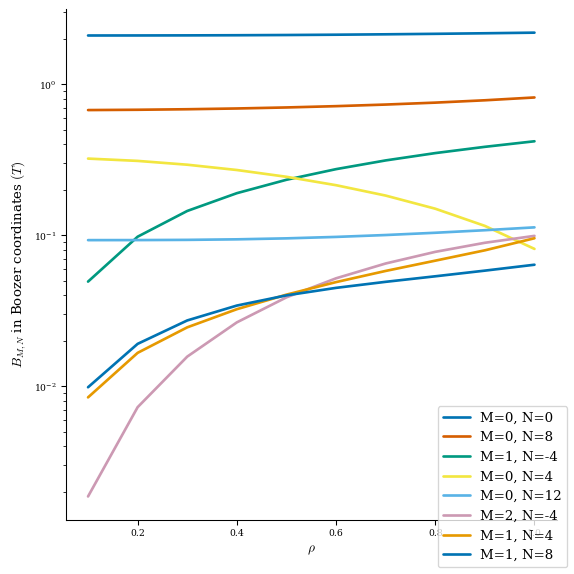
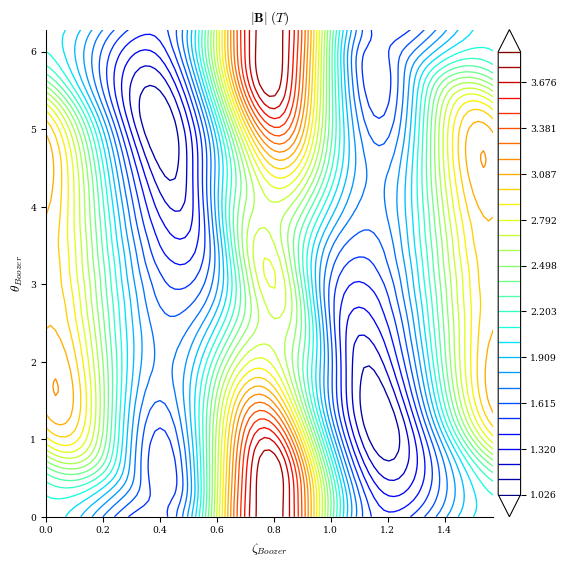
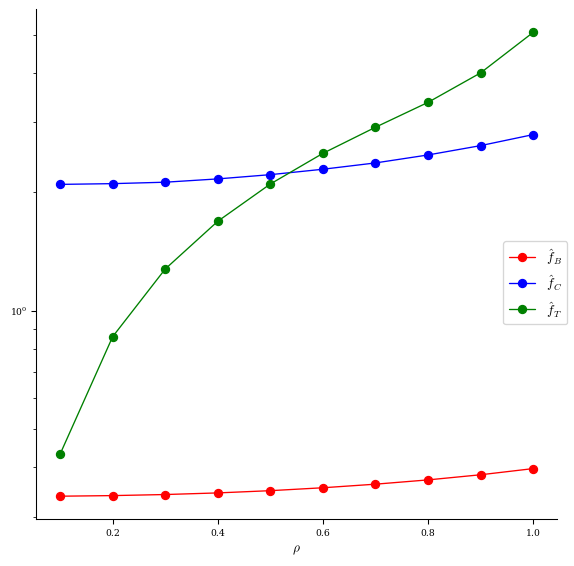
QS metrics
The last plot shows the three different QS errors implemented in DESC. Their definitions and the normalized scalar quantities plotted for each flux surface are shown below:
Boozer Coordinates
This is the “traditional” definition of QS. The drawbacks of this metric are that Boozer coordinates are expensive to compute, and it only provides “global” information about the error on each surface. But it has the nice property of \(\hat{f}_B \in [0,1]\).
\begin{equation} |\mathbf{B}| = B(\psi, M\vartheta_{B} - N\zeta_{B}) \end{equation}
\begin{equation} \mathbf{f}_{B} = \{ B_{mn} ~|~ m/n \neq M/N \} \end{equation}
\begin{equation} \hat{f}_{B} = \frac{|\mathbf{f}_{B}|}{\sqrt{\sum_{m,n} B_{mn}^2}} \end{equation}
Two-Term
This definition is advantageous because it does not require a transformation to Boozer coordinates, and it reveals “local” errors within a flux surface.
\begin{equation} f_{C} = \left( M \iota - N \right) \left( \mathbf{B} \times \nabla \psi \right) \cdot \nabla B - \left( M G + N I \right) \mathbf{B} \cdot \nabla B. \end{equation}
\begin{equation} \mathbf{f}_{C} = \{ f_{C}(\theta_{i},\zeta_{j}) ~|~ i \in [0,2\pi), j \in [0,2\pi/N_{FP}) \} \end{equation}
\begin{equation} \hat{f}_{C} = \frac{\langle |f_C| \rangle}{\langle B \rangle^3}. \end{equation}
Triple Product
This is also a local error metric that can be evaluated without Boozer coordinates. The potential advantages of this definition are that it does not require specifying the helicity (type of quasi-symmetry) and does not assume \(\mathbf{J}\cdot\nabla\psi=0\).
\begin{equation} f_{T} = \nabla \psi \times \nabla B \cdot \nabla \left( \mathbf{B} \cdot \nabla B \right) \end{equation}
\begin{equation} \mathbf{f}_{T} = \{ f_{T}(\theta_{i},\zeta_{j}) ~|~ i \in [0,2\pi), j \in [0,2\pi/N_{FP}) \} \end{equation}
\begin{equation} \hat{f}_{T}(\psi) = \frac{\langle R \rangle^2 \langle |f_{T}| \rangle}{\langle B \rangle^4} \end{equation}
Optimizer
To set up the optimization problem, we need to choose an optimization algorithm. "proximal-lsq-exact" is a custom least-squares routine (with proximal referring to the proximal projection done at each step to ensure force balance i.e. it perturbs the boundary in the direction to optimize the objective function, then resolves the equilibrium to ensure force balance), but there are other options available (see
documentation).
[7]:
optimizer = Optimizer("proximal-lsq-exact")
Specifying constraints
Next we need to define the optimization constraints. In DESC, we explicitly specify the constraints, and all other parameters become free variables for optimization. In this example, we would like the following 4 stellarator-symmetric boundary coefficients to be our only optimization variables:
\(R^{b}_{1,2} \cos(\theta) \cos(2N_{FP}\phi)\)
\(R^{b}_{-1,-2} \sin(\theta) \sin(2N_{FP}\phi)\)
\(Z^{b}_{-1,2} \sin(\theta) \cos(2N_{FP}\phi)\)
\(Z^{b}_{1,-2} \cos(\theta) \sin(2N_{FP}\phi)\)
We will fix all other boundary modes besides these. We will also fix the pressure profile, rotational transform profile, and total toroidal magnetic flux. Finally, we also specify equilibrium force balance as a constraint by including the ForceBalance() objective in the list of constraints.
[8]:
# indices of boundary modes we want to optimize
idx_Rcc = eq_init.surface.R_basis.get_idx(M=1, N=2)
idx_Rss = eq_init.surface.R_basis.get_idx(M=-1, N=-2)
idx_Zsc = eq_init.surface.Z_basis.get_idx(M=-1, N=2)
idx_Zcs = eq_init.surface.Z_basis.get_idx(M=1, N=-2)
print("surface.R_basis.modes is an array of [l,m,n] of the surface modes:")
print(eq_init.surface.R_basis.modes[0:10])
# boundary modes to constrain
R_modes = np.delete(eq_init.surface.R_basis.modes, [idx_Rcc, idx_Rss], axis=0)
Z_modes = np.delete(eq_init.surface.Z_basis.modes, [idx_Zsc, idx_Zcs], axis=0)
eq_qs_T = eq_init.copy() # make a copy of the original one
# constraints
constraints = (
ForceBalance(eq=eq_qs_T), # enforce JxB-grad(p)=0 during optimization
FixBoundaryR(eq=eq_qs_T, modes=R_modes), # fix specified R boundary modes
FixBoundaryZ(eq=eq_qs_T, modes=Z_modes), # fix specified Z boundary modes
FixPressure(eq=eq_qs_T), # fix pressure profile
FixIota(eq=eq_qs_T), # fix rotational transform profile
FixPsi(eq=eq_qs_T), # fix total toroidal magnetic flux
)
surface.R_basis.modes is an array of [l,m,n] of the surface modes:
[[ 0 -8 -4]
[ 0 -7 -4]
[ 0 -6 -4]
[ 0 -5 -4]
[ 0 -4 -4]
[ 0 -3 -4]
[ 0 -2 -4]
[ 0 -1 -4]
[ 0 -8 -3]
[ 0 -7 -3]]
Optimizing for Triple Product QS in Volume
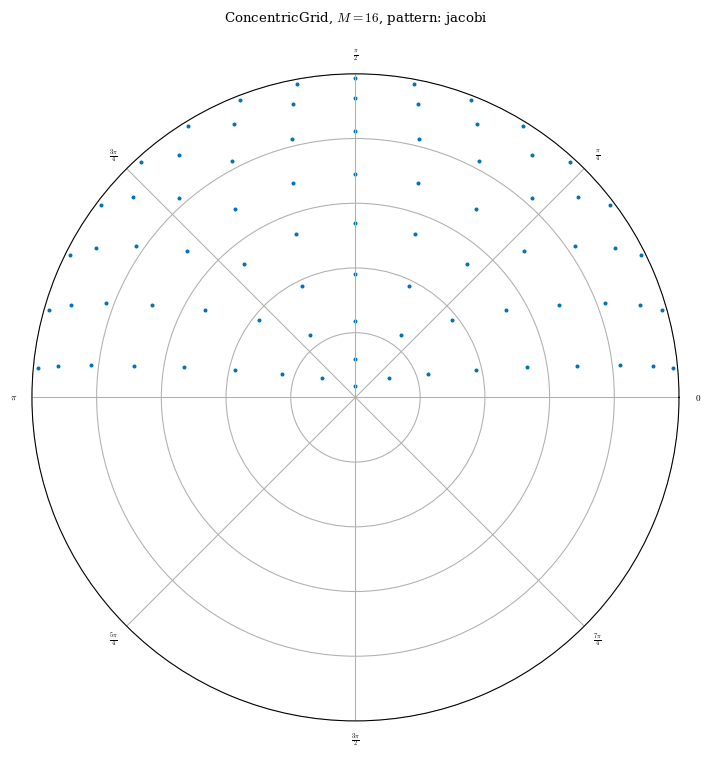
First we are going to optimize for QS using the “triple product” objective, evaluated throughout the plasma volume. We start by creating the grid of collocation points where we want the \(f_T\) errors to be evaluated. We then initialize the appropriate objective function with this grid.
[9]:
# objective
grid_vol = ConcentricGrid(
L=eq_init.L_grid,
M=eq_init.M_grid,
N=eq_init.N_grid,
NFP=eq_init.NFP,
sym=eq_init.sym,
)
plot_grid(grid_vol, figsize=(8, 8))
objective_fT = ObjectiveFunction(QuasisymmetryTripleProduct(eq=eq_qs_T, grid=grid_vol))
We are now ready to run the optimization problem. The syntax is shown below with many of the optimization options that are available – you can try changing these parameters.
[10]:
eq_qs_T, result_T = eq_qs_T.optimize(
objective=objective_fT,
constraints=constraints,
optimizer=optimizer,
ftol=5e-2, # stopping tolerance on the function value
xtol=1e-6, # stopping tolerance on the step size
gtol=1e-6, # stopping tolerance on the gradient
maxiter=50, # maximum number of iterations
options={
"perturb_options": {"order": 2, "verbose": 0}, # use 2nd-order perturbations
"solve_options": {
"ftol": 5e-3,
"xtol": 1e-6,
"gtol": 1e-6,
"verbose": 0,
}, # for equilibrium subproblem
},
copy=False, # copy=False we will overwrite the eq_qs_T object with the optimized result
verbose=3,
)
Building objective: QS triple product
Precomputing transforms
Timer: Precomputing transforms = 2.23 sec
Timer: Objective build = 4.54 sec
Building objective: force
Precomputing transforms
Timer: Precomputing transforms = 1.19 sec
Timer: Objective build = 1.69 sec
Timer: Proximal projection build = 16.4 sec
Timer: Linear constraint projection build = 4.42 sec
Compiling objective function and derivatives: ['QS triple product']
Timer: Objective compilation time = 6.33 sec
Timer: Jacobian compilation time = 15.6 sec
Timer: Total compilation time = 22.0 sec
Compiling objective function and derivatives: ['force']
Timer: Objective compilation time = 3.62 sec
Timer: Jacobian compilation time = 9.29 sec
Timer: Total compilation time = 12.9 sec
Number of parameters: 4
Number of objectives: 1377
Starting optimization
Using method: proximal-lsq-exact
Iteration Total nfev Cost Cost reduction Step norm Optimality
0 1 6.409e+01 7.916e+03
1 2 2.066e+01 4.344e+01 2.078e-02 2.529e+03
2 3 3.243e+00 1.741e+01 3.604e-02 4.044e+02
3 4 4.970e-01 2.746e+00 4.288e-02 6.251e+01
4 5 6.229e-02 4.347e-01 3.349e-02 1.010e+01
5 6 4.948e-03 5.735e-02 2.054e-02 1.503e+00
6 7 1.545e-03 3.403e-03 1.200e-02 1.082e-01
7 8 1.523e-03 2.198e-05 8.282e-04 1.137e-03
Optimization terminated successfully.
`ftol` condition satisfied.
Current function value: 1.523e-03
Total delta_x: 1.072e-01
Iterations: 7
Function evaluations: 8
Jacobian evaluations: 8
Timer: Solution time = 3.84 min
Timer: Avg time per step = 28.8 sec
Start of solver
Total (sum of squares): 6.409e+01,
Maximum absolute Quasi-symmetry error: 4.730e+02 (T^4/m^2)
Minimum absolute Quasi-symmetry error: 4.422e-04 (T^4/m^2)
Average absolute Quasi-symmetry error: 1.117e+01 (T^4/m^2)
Maximum absolute Quasi-symmetry error: 4.183e+00 (normalized)
Minimum absolute Quasi-symmetry error: 3.910e-06 (normalized)
Average absolute Quasi-symmetry error: 9.879e-02 (normalized)
Maximum absolute Force error: 1.516e+05 (N)
Minimum absolute Force error: 2.431e+00 (N)
Average absolute Force error: 5.922e+03 (N)
Maximum absolute Force error: 8.198e-03 (normalized)
Minimum absolute Force error: 1.315e-07 (normalized)
Average absolute Force error: 3.203e-04 (normalized)
R boundary error: 0.000e+00 (m)
Z boundary error: 0.000e+00 (m)
Fixed-pressure profile error: 0.000e+00 (Pa)
Fixed-iota profile error: 0.000e+00 (dimensionless)
Fixed-Psi error: 0.000e+00 (Wb)
End of solver
Total (sum of squares): 1.523e-03,
Maximum absolute Quasi-symmetry error: 2.085e+00 (T^4/m^2)
Minimum absolute Quasi-symmetry error: 1.884e-05 (T^4/m^2)
Average absolute Quasi-symmetry error: 1.081e-01 (T^4/m^2)
Maximum absolute Quasi-symmetry error: 1.844e-02 (normalized)
Minimum absolute Quasi-symmetry error: 1.666e-07 (normalized)
Average absolute Quasi-symmetry error: 9.560e-04 (normalized)
Maximum absolute Force error: 1.640e+04 (N)
Minimum absolute Force error: 3.549e-01 (N)
Average absolute Force error: 7.465e+02 (N)
Maximum absolute Force error: 8.868e-04 (normalized)
Minimum absolute Force error: 1.919e-08 (normalized)
Average absolute Force error: 4.038e-05 (normalized)
R boundary error: 6.939e-18 (m)
Z boundary error: 3.957e-27 (m)
Fixed-pressure profile error: 0.000e+00 (Pa)
Fixed-iota profile error: 0.000e+00 (dimensionless)
Fixed-Psi error: 0.000e+00 (Wb)
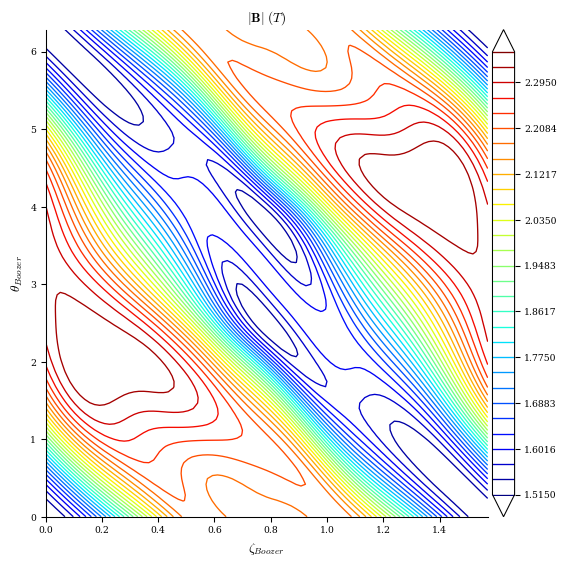
Let us plot the QS errors again to see how well the optimization worked:
[11]:
plot_boozer_surface(eq_qs_T); # |B| contours at rho=1 surface
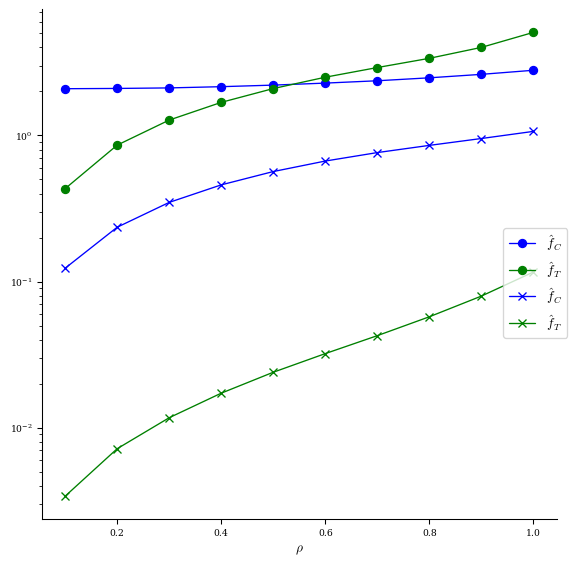
[12]:
# compare f_T & f_C before (o) vs after (x) optimization
fig, ax = plot_qs_error(
eq_init, helicity=(1, eq_init.NFP), fB=False, legend=False, rho=10
)
plot_qs_error(
eq_qs_T, helicity=(1, eq_init.NFP), fB=False, ax=ax, marker=["x", "x"], rho=10
);
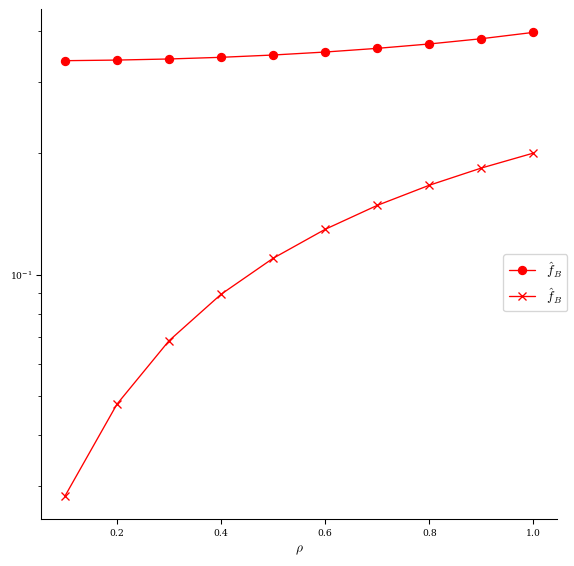
[13]:
# compare f_B before (o) vs after (x) optimization
fig, ax = plot_qs_error(
eq_init, helicity=(1, eq_init.NFP), fT=False, fC=False, legend=False, rho=10
)
plot_qs_error(
eq_qs_T, helicity=(1, eq_init.NFP), fT=False, fC=False, ax=ax, marker=["x"], rho=10
);
Optimizing for Two-Term QH at Boundary Surface
Next we are going to optimize for QH using the “two-term” objective, evaluated at the \(\rho=1\) flux surface. Again we need to create the grid of collocation points where we want the \(f_C\) errors to be evaluated. We then initialize the appropriate objective function with this grid.
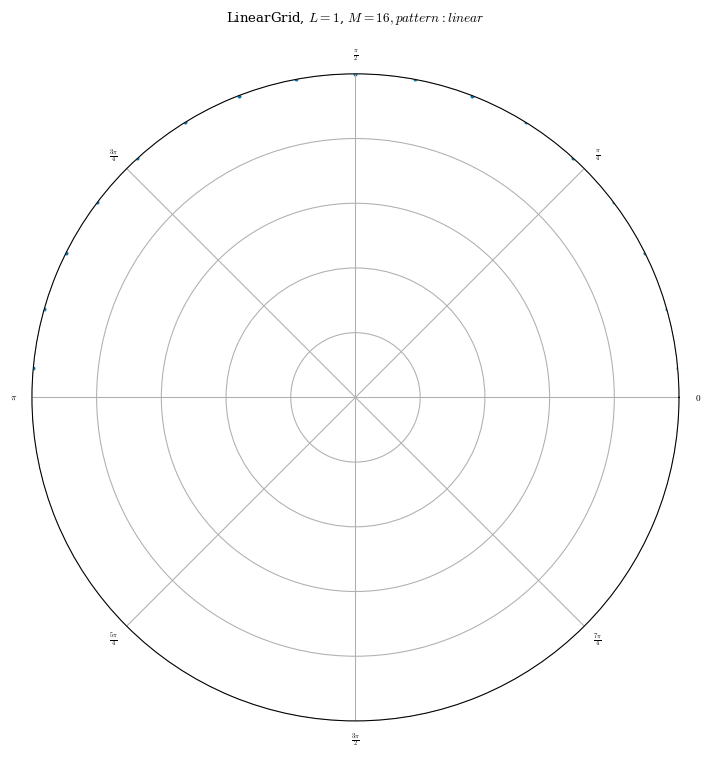
[14]:
grid_rho1 = LinearGrid(
M=eq_init.M_grid,
N=eq_init.N_grid,
NFP=eq_init.NFP,
sym=eq_init.sym,
rho=np.array(1.0),
)
plot_grid(grid_rho1, figsize=(8, 8))
eq_qs_C = eq_init.copy()
# constraints
constraints = (
ForceBalance(eq=eq_qs_C), # enforce JxB-grad(p)=0 during optimization
FixBoundaryR(eq=eq_qs_C, modes=R_modes), # fix specified R boundary modes
FixBoundaryZ(eq=eq_qs_C, modes=Z_modes), # fix specified Z boundary modes
FixPressure(eq=eq_qs_C), # fix pressure profile
FixIota(eq=eq_qs_C), # fix rotational transform profile
FixPsi(eq=eq_qs_C), # fix total toroidal magnetic flux
)
# two-term objective
objective_fC = ObjectiveFunction(
QuasisymmetryTwoTerm(eq=eq_qs_C, grid=grid_rho1, helicity=(1, eq_init.NFP))
)
Now we can re-run the optimization from the same intial guess as before, but using this different objective function. We can reuse the same optimizer from the first run.
[15]:
eq_qs_C, result_C = eq_qs_C.optimize(
objective=objective_fC,
constraints=constraints,
optimizer=optimizer,
ftol=1e-2,
xtol=1e-6,
gtol=1e-6,
maxiter=50,
options={
"perturb_options": {"order": 2, "verbose": 0},
"solve_options": {"ftol": 1e-2, "xtol": 1e-6, "gtol": 1e-6, "verbose": 0},
},
copy=False,
verbose=3,
)
Building objective: QS two-term
Precomputing transforms
Timer: Precomputing transforms = 399 ms
Timer: Objective build = 1.23 sec
Building objective: force
Precomputing transforms
Timer: Precomputing transforms = 567 ms
Timer: Objective build = 1.27 sec
Timer: Proximal projection build = 6.24 sec
Timer: Linear constraint projection build = 2.98 sec
Compiling objective function and derivatives: ['QS two-term']
Timer: Objective compilation time = 3.50 sec
Timer: Jacobian compilation time = 19.5 sec
Timer: Total compilation time = 23.0 sec
Compiling objective function and derivatives: ['force']
Timer: Objective compilation time = 5.97 sec
Timer: Jacobian compilation time = 12.0 sec
Timer: Total compilation time = 18.0 sec
Number of parameters: 4
Number of objectives: 289
Starting optimization
Using method: proximal-lsq-exact
Iteration Total nfev Cost Cost reduction Step norm Optimality
0 1 1.957e+04 8.707e+05
1 2 1.366e+04 5.917e+03 1.073e-02 5.735e+05
2 3 6.926e+03 6.729e+03 2.221e-02 2.656e+05
3 4 2.297e+03 4.629e+03 5.120e-02 6.051e+04
4 5 1.535e+03 7.620e+02 5.187e-02 5.600e+03
5 6 1.516e+03 1.898e+01 4.711e-03 6.688e+02
6 7 1.513e+03 2.768e+00 1.073e-03 1.926e+02
Optimization terminated successfully.
`ftol` condition satisfied.
Current function value: 1.513e+03
Total delta_x: 1.184e-01
Iterations: 6
Function evaluations: 7
Jacobian evaluations: 7
Timer: Solution time = 2.44 min
Timer: Avg time per step = 20.9 sec
Start of solver
Total (sum of squares): 1.957e+04,
Maximum absolute Quasi-symmetry (1,4.0) two-term error: 1.353e+02 (T^3)
Minimum absolute Quasi-symmetry (1,4.0) two-term error: 1.562e-02 (T^3)
Average absolute Quasi-symmetry (1,4.0) two-term error: 2.315e+01 (T^3)
Maximum absolute Quasi-symmetry (1,4.0) two-term error: 2.034e+01 (normalized)
Minimum absolute Quasi-symmetry (1,4.0) two-term error: 2.348e-03 (normalized)
Average absolute Quasi-symmetry (1,4.0) two-term error: 3.479e+00 (normalized)
Maximum absolute Force error: 1.516e+05 (N)
Minimum absolute Force error: 2.431e+00 (N)
Average absolute Force error: 5.922e+03 (N)
Maximum absolute Force error: 8.198e-03 (normalized)
Minimum absolute Force error: 1.315e-07 (normalized)
Average absolute Force error: 3.203e-04 (normalized)
R boundary error: 0.000e+00 (m)
Z boundary error: 0.000e+00 (m)
Fixed-pressure profile error: 0.000e+00 (Pa)
Fixed-iota profile error: 0.000e+00 (dimensionless)
Fixed-Psi error: 0.000e+00 (Wb)
End of solver
Total (sum of squares): 1.513e+03,
Maximum absolute Quasi-symmetry (1,4.0) two-term error: 2.017e+01 (T^3)
Minimum absolute Quasi-symmetry (1,4.0) two-term error: 7.090e-02 (T^3)
Average absolute Quasi-symmetry (1,4.0) two-term error: 7.306e+00 (T^3)
Maximum absolute Quasi-symmetry (1,4.0) two-term error: 3.031e+00 (normalized)
Minimum absolute Quasi-symmetry (1,4.0) two-term error: 1.065e-02 (normalized)
Average absolute Quasi-symmetry (1,4.0) two-term error: 1.098e+00 (normalized)
Maximum absolute Force error: 1.993e+04 (N)
Minimum absolute Force error: 4.870e-01 (N)
Average absolute Force error: 9.949e+02 (N)
Maximum absolute Force error: 1.078e-03 (normalized)
Minimum absolute Force error: 2.634e-08 (normalized)
Average absolute Force error: 5.381e-05 (normalized)
R boundary error: 6.939e-18 (m)
Z boundary error: 3.957e-27 (m)
Fixed-pressure profile error: 0.000e+00 (Pa)
Fixed-iota profile error: 0.000e+00 (dimensionless)
Fixed-Psi error: 0.000e+00 (Wb)
Let us plot the QS errors again for this case. Was one objective more effective than the other at improving quasi-symmetry for this example?
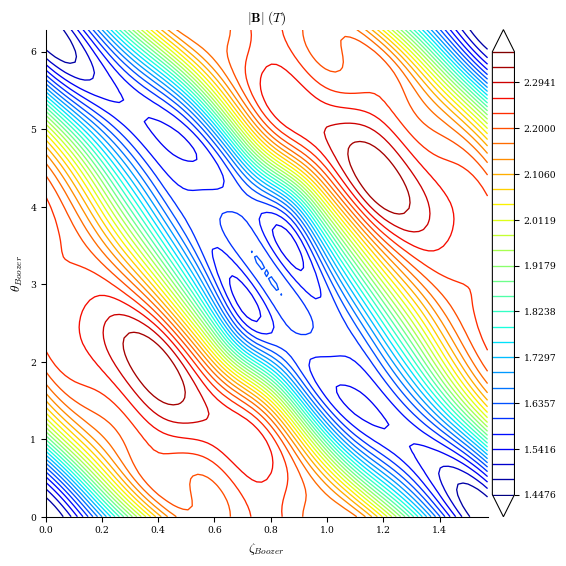
[16]:
plot_boozer_surface(eq_qs_C); # |B| contours at rho=1 surface
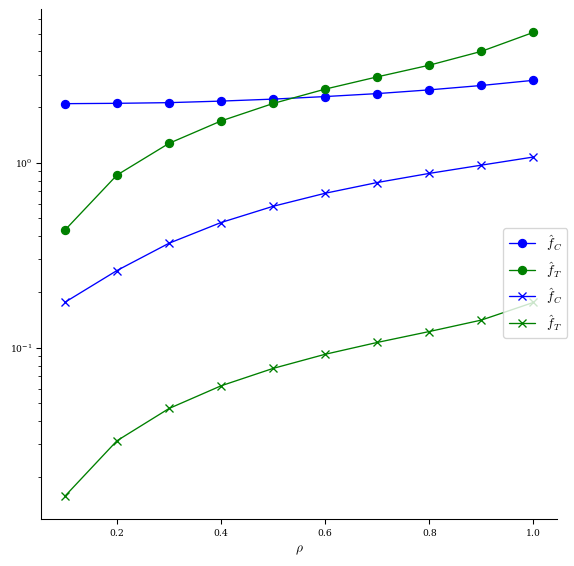
[17]:
# compare f_T & f_C before (o) vs after (x) optimization
fig, ax = plot_qs_error(
eq_init, helicity=(1, eq_init.NFP), fB=False, legend=False, rho=10
)
plot_qs_error(
eq_qs_C, helicity=(1, eq_init.NFP), fB=False, ax=ax, marker=["x", "x"], rho=10
);
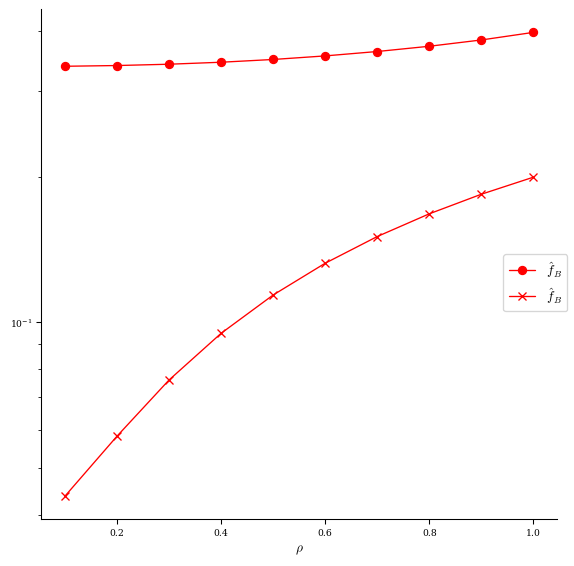
[18]:
# compare f_B before (o) vs after (x) optimization
fig, ax = plot_qs_error(
eq_init, helicity=(1, eq_init.NFP), fT=False, fC=False, legend=False, rho=10
)
plot_qs_error(
eq_qs_C, helicity=(1, eq_init.NFP), fT=False, fC=False, ax=ax, marker=["x"], rho=10
);
Combining Multiple Objectives
It is very easy in DESC to combine multiple optimization objectives with relative weights between them. Here is an example of how to create an objective optimizing for both \(f_B\) and a target aspect ratio:
[19]:
objective = ObjectiveFunction(
(
QuasisymmetryBoozer(eq=eq_init, helicity=(1, eq_init.NFP), weight=1e-2),
AspectRatio(eq=eq_init, target=6, weight=1e1),
)
)