Zernike Polynomial Evaluation

This notebook compares different methods for evaluating the radial part of the Zernike polynomials, in terms of both speed and accuracy

The two primary methods we consider are direct polynomial evaluation using Horner’s method and an evaluation scheme based on a recurrence relation for Jacobi polynomials.

The radial part of the Zernike polynomials is given by

\[\mathcal{R}_l^{|m|} (\rho) = \sum_{s=0}^{(l-|m|)/2} \frac{(-1)^s(l-s)!}{ s!\left( \cfrac{l+|m|}{2} - s\right)! \left( \cfrac{l-|m|}{2} + s\right)! } \rho^{l-2s}\]

Because the coefficient of rho is made up of entirely integer operations, it can be evaluated quickly and exactly to arbitrary orders (recall that python natively supports arbitrary length integer arithmetic). These coefficients can then be evaluated using Horner’s method. This is done in the zernike_radial_poly function.

The other approach uses the fact that the above equation can be written as

\[\mathcal{R}_l^{m} (\rho) = (-1)^{(l-m)/2} \rho^m P_{(l-m)/2}^{m, 0} (1 - 2 \rho^2) \hspace{1cm}\text{for } m\geq0\]

where \(P_{n}^{\alpha, \beta}(\rho)\) is a Jacobi polynomial. This allows us to use stable recurrence relations for the Jacobi polynomials, as is done in the zernike_radial function.

The recurrence relationship for the Jacobi polynomials is,

\[2n(c-n)(c-2)P_{n}^{\alpha,\beta}(\rho) = (c-1)[c(c-2)\rho + (a-b)(c-2n)]P_{n-1}^{\alpha,\beta}(\rho) - 2(a-1)(b-1)cP_{n-2}^{\alpha,\beta}(\rho)\]

where

\[c = 2n + \alpha + \beta, \hspace{1cm} a = n +\alpha, \hspace{1cm} b = n + \beta\]

For the derivatives of Zernike Radial part, we will also need derivatives of Jacobi polynomials, for which there exist another relation.

\[\cfrac{d^k}{dx^k} P_n^{(\alpha, \beta)}(x) = \cfrac{\Gamma(\alpha + \beta + n + 1 + k)}{2^k\Gamma(\alpha + \beta + n + 1)} P_{n-k}^{(\alpha + k, \beta + k)}(x)\]

This function relates the derivatives to normal Jacobi function, and we can use above recursion relation to calculate derivatives.

[1]:

import sys
import os

sys.path.insert(0, os.path.abspath("."))
sys.path.append(os.path.abspath("../../"))

[2]:

import numpy as np
import mpmath
import matplotlib
import matplotlib.pyplot as plt
from desc.basis import (
    polyder_vec,
    ZernikePolynomial,
    zernike_radial,
    zernike_radial_coeffs,
    zernike_radial_poly,
)

DESC version 0.10.4+123.g1cd83e9f,using JAX backend, jax version=0.4.14, jaxlib version=0.4.14, dtype=float64
Using device: CPU, with 8.92 GB available memory

[3]:

basis = ZernikePolynomial(L=50, M=50, spectral_indexing="ansi", sym="cos")
r = np.linspace(0, 1, 100)

Here we time the evaluation for a basis set containing 676 modes on a grid of 100 points, for derivative orders 0 through 3. (note the block_until_ready is needed to get accurate timing with jax)

[4]:

print("zernike_radial, 0th derivative")
%timeit -n 1000 _ = zernike_radial(r, basis.modes[:,0], basis.modes[:,1], 0).block_until_ready()
print("zernike_radial, 1st derivative")
%timeit -n 1000 _ = zernike_radial(r, basis.modes[:,0], basis.modes[:,1], 1).block_until_ready()
print("zernike_radial, 2nd derivative")
%timeit -n 1000 _ = zernike_radial(r, basis.modes[:,0], basis.modes[:,1], 2).block_until_ready()
print("zernike_radial, 3rd derivative")
%timeit -n 1000 _ = zernike_radial(r, basis.modes[:,0], basis.modes[:,1], 3).block_until_ready()

zernike_radial, 0th derivative
2.4 ms ± 1.34 ms per loop (mean ± std. dev. of 7 runs, 1,000 loops each)
zernike_radial, 1st derivative
3.74 ms ± 41.6 µs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)
zernike_radial, 2nd derivative
3.04 ms ± 18.6 µs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)
zernike_radial, 3rd derivative
2.94 ms ± 11.3 µs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)

[6]:

print("zernike_radial_poly, 0th derivative")
%timeit -n 100 _ = zernike_radial_poly(r[:,np.newaxis], basis.modes[:,0], basis.modes[:,1], dr=0, exact=False)
print("zernike_radial_poly, 1st derivative")
%timeit -n 100 _ = zernike_radial_poly(r[:,np.newaxis], basis.modes[:,0], basis.modes[:,1], dr=1, exact=False)
print("zernike_radial_poly, 2nd derivative")
%timeit -n 100 _ = zernike_radial_poly(r[:,np.newaxis], basis.modes[:,0], basis.modes[:,1], dr=2, exact=False)
print("zernike_radial_poly, 3rd derivative")
%timeit -n 100 _ = zernike_radial_poly(r[:,np.newaxis], basis.modes[:,0], basis.modes[:,1], dr=3, exact=False)

zernike_radial_poly, 0th derivative
26.5 ms ± 1.11 ms per loop (mean ± std. dev. of 7 runs, 100 loops each)
zernike_radial_poly, 1st derivative
26.4 ms ± 971 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
zernike_radial_poly, 2nd derivative
26.3 ms ± 1.61 ms per loop (mean ± std. dev. of 7 runs, 100 loops each)
zernike_radial_poly, 3rd derivative
28.5 ms ± 2 ms per loop (mean ± std. dev. of 7 runs, 100 loops each)

We see that the implementation using Jacobi polynomial recurrence relation is significantly faster, despite the overhead from the JAX just-in-time compiler

For accuracy comparison, we will also evaluate the Zernike radial polynomials in extended precision (100 digits of accuracy) and treat this as the “true” value.

[7]:

mpmath.mp.dps = 100
c = zernike_radial_coeffs(basis.modes[:, 0], basis.modes[:, 1], exact=True)

print("zernike_radial_exact, 0th derivative")
%time zt0 = np.array([np.asarray(mpmath.polyval(list(ci), r), dtype=float) for ci in c]).T
print("zernike_radial_exact, 1st derivative")
%time zt1 = np.array([np.asarray(mpmath.polyval(list(ci), r), dtype=float) for ci in polyder_vec(c, 1, exact=True)]).T
print("zernike_radial_exact, 2nd derivative")
%time zt2 = np.array([np.asarray(mpmath.polyval(list(ci), r), dtype=float) for ci in polyder_vec(c, 2, exact=True)]).T
print("zernike_radial_exact, 3rd derivative")
%time zt3 = np.array([np.asarray(mpmath.polyval(list(ci), r), dtype=float) for ci in polyder_vec(c, 3, exact=True)]).T

zernike_radial_exact, 0th derivative

CPU times: user 9.55 s, sys: 5.15 ms, total: 9.56 s
Wall time: 9.65 s
zernike_radial_exact, 1st derivative
CPU times: user 9.38 s, sys: 9.25 ms, total: 9.39 s
Wall time: 9.41 s
zernike_radial_exact, 2nd derivative
CPU times: user 9.31 s, sys: 875 µs, total: 9.31 s
Wall time: 9.31 s
zernike_radial_exact, 3rd derivative
CPU times: user 9.42 s, sys: 518 µs, total: 9.42 s
Wall time: 9.44 s

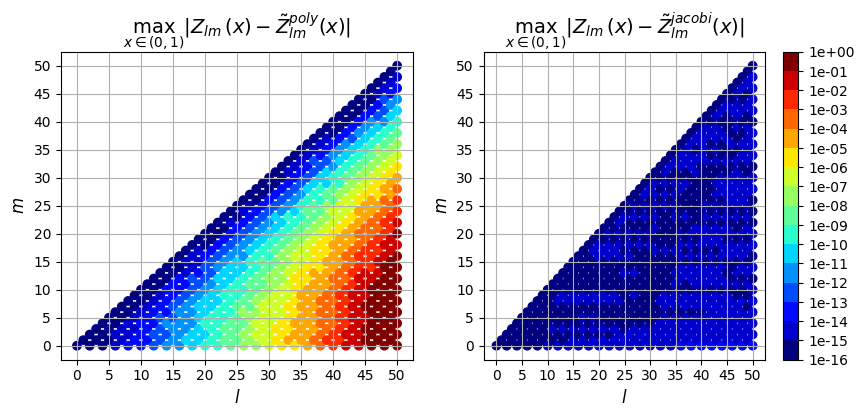
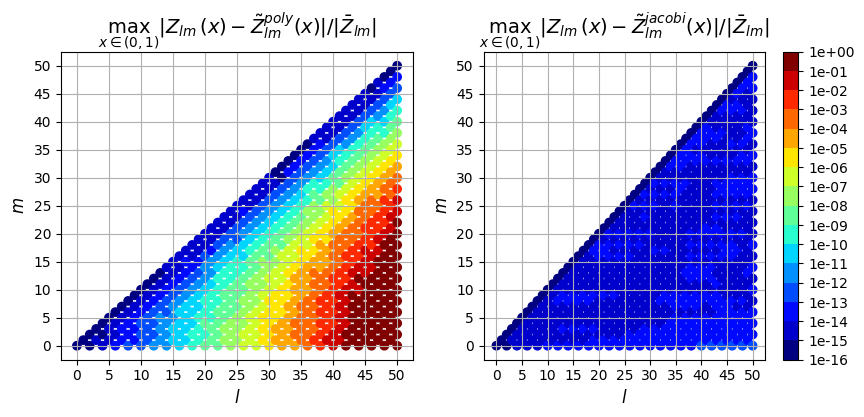
Next we can plot the error resulting from the two evaluation methods (polynomial evaluation and jacobi recurrence relation) vs the true solution computed in exact arithmetic. We plot the max absolute error as well as the max relative error over \(\rho \in (0,1)\) for each derivative order.

[8]:

zr0 = zernike_radial(r, basis.modes[:, 0], basis.modes[:, 1], 0)
zr1 = zernike_radial(r, basis.modes[:, 0], basis.modes[:, 1], 1)
zr2 = zernike_radial(r, basis.modes[:, 0], basis.modes[:, 1], 2)
zr3 = zernike_radial(r, basis.modes[:, 0], basis.modes[:, 1], 3)
zp0 = zernike_radial_poly(
    r[:, np.newaxis], basis.modes[:, 0], basis.modes[:, 1], dr=0, exact=False
)
zp1 = zernike_radial_poly(
    r[:, np.newaxis], basis.modes[:, 0], basis.modes[:, 1], dr=1, exact=False
)
zp2 = zernike_radial_poly(
    r[:, np.newaxis], basis.modes[:, 0], basis.modes[:, 1], dr=2, exact=False
)
zp3 = zernike_radial_poly(
    r[:, np.newaxis], basis.modes[:, 0], basis.modes[:, 1], dr=3, exact=False
)

[9]:

cmap = plt.cm.jet  # define the colormap
# extract all colors from the .jet map
cmaplist = [cmap(i) for i in range(cmap.N)]

# create the new map
cmap = matplotlib.colors.LinearSegmentedColormap.from_list(
    "Custom cmap", cmaplist, cmap.N
)

# define the bins and normalize
bounds = np.logspace(-16, 0, 17)
norm = matplotlib.colors.BoundaryNorm(bounds, cmap.N)

Absolute Error

0th derivative

[10]:

fig, ax = plt.subplots(1, 2, squeeze=True, figsize=(10, 4))
im = ax[0].scatter(
    basis.modes[:, 0],
    basis.modes[:, 1],
    c=np.max(abs(zp0 - zt0), axis=0),
    norm=norm,
    cmap=cmap,
)
im = ax[1].scatter(
    basis.modes[:, 0],
    basis.modes[:, 1],
    c=np.max(abs(zr0 - zt0), axis=0),
    norm=norm,
    cmap=cmap,
)
cbar = fig.colorbar(im, ticks=bounds)
cbar.ax.set_yticklabels(["{:.0e}".format(foo) for foo in bounds])
ax[0].grid(True)
ax[1].grid(True)
ax[0].set_xticks(np.arange(0, 55, 5))
ax[0].set_yticks(np.arange(0, 55, 5))
ax[1].set_xticks(np.arange(0, 55, 5))
ax[1].set_yticks(np.arange(0, 55, 5))
ax[0].set_xlabel("$l$", fontsize=12)
ax[0].set_ylabel("$m$", fontsize=12)
ax[1].set_xlabel("$l$", fontsize=12)
ax[1].set_ylabel("$m$", fontsize=12)
ax[0].set_title(
    "$\max_{x \in (0,1)} |Z_{lm}(x) - \\tilde{Z}_{lm}^{poly}(x)|$", fontsize=14
)
ax[1].set_title(
    "$\max_{x \in (0,1)} |Z_{lm}(x) - \\tilde{Z}_{lm}^{jacobi}(x)|$", fontsize=14
);

../_images/notebooks_zernike_eval_16_0.png

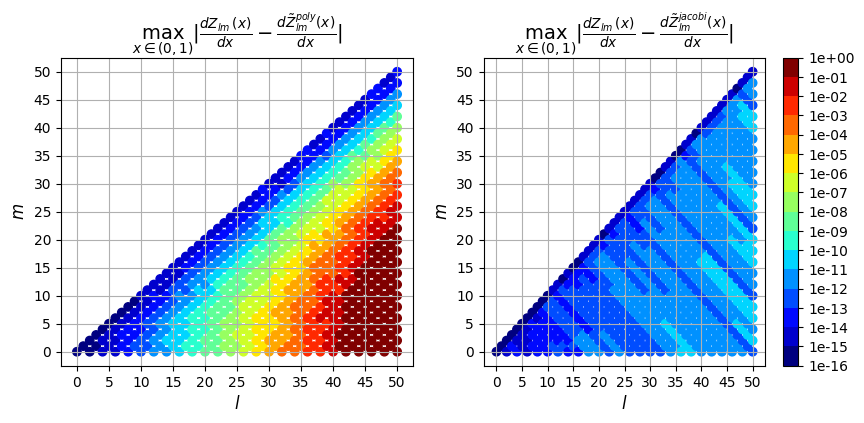
1st derivative

[11]:

fig, ax = plt.subplots(1, 2, squeeze=True, figsize=(10, 4))
im = ax[0].scatter(
    basis.modes[:, 0],
    basis.modes[:, 1],
    c=np.max(abs(zp1 - zt1), axis=0),
    norm=norm,
    cmap=cmap,
)
im = ax[1].scatter(
    basis.modes[:, 0],
    basis.modes[:, 1],
    c=np.max(abs(zr1 - zt1), axis=0),
    norm=norm,
    cmap=cmap,
)
cbar = fig.colorbar(im, ticks=bounds)
cbar.ax.set_yticklabels(["{:.0e}".format(foo) for foo in bounds])
ax[0].grid(True)
ax[1].grid(True)
ax[0].set_xticks(np.arange(0, 55, 5))
ax[0].set_yticks(np.arange(0, 55, 5))
ax[1].set_xticks(np.arange(0, 55, 5))
ax[1].set_yticks(np.arange(0, 55, 5))
ax[0].set_xlabel("$l$", fontsize=12)
ax[0].set_ylabel("$m$", fontsize=12)
ax[1].set_xlabel("$l$", fontsize=12)
ax[1].set_ylabel("$m$", fontsize=12)
ax[0].set_title(
    "$\max_{x \in (0,1)} |\\frac{dZ_{lm}(x)}{dx} - \\frac{d\\tilde{Z}_{lm}^{poly}(x)}{dx}|$",
    fontsize=14,
)
ax[1].set_title(
    "$\max_{x \in (0,1)} |\\frac{dZ_{lm}(x)}{dx} - \\frac{d\\tilde{Z}_{lm}^{jacobi}(x)}{dx}|$",
    fontsize=14,
);

../_images/notebooks_zernike_eval_18_0.png

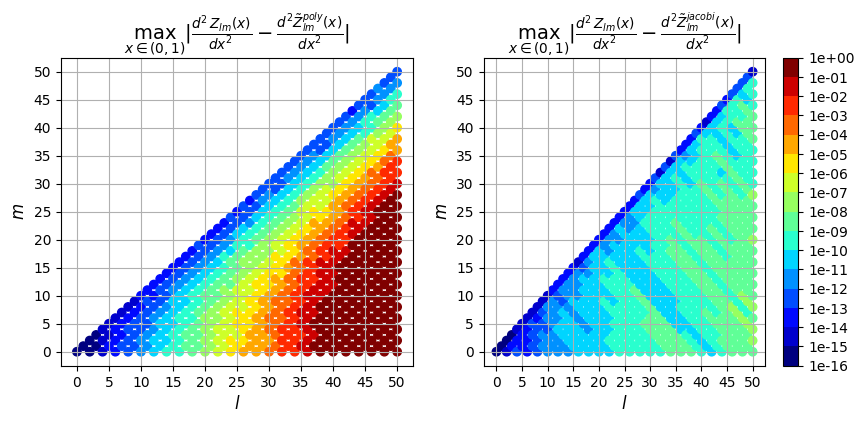
2nd derivative

[12]:

fig, ax = plt.subplots(1, 2, squeeze=True, figsize=(10, 4))
im = ax[0].scatter(
    basis.modes[:, 0],
    basis.modes[:, 1],
    c=np.max(abs(zp2 - zt2), axis=0),
    norm=norm,
    cmap=cmap,
)
im = ax[1].scatter(
    basis.modes[:, 0],
    basis.modes[:, 1],
    c=np.max(abs(zr2 - zt2), axis=0),
    norm=norm,
    cmap=cmap,
)
cbar = fig.colorbar(im, ticks=bounds)
cbar.ax.set_yticklabels(["{:.0e}".format(foo) for foo in bounds])
ax[0].grid(True)
ax[1].grid(True)
ax[0].set_xticks(np.arange(0, 55, 5))
ax[0].set_yticks(np.arange(0, 55, 5))
ax[1].set_xticks(np.arange(0, 55, 5))
ax[1].set_yticks(np.arange(0, 55, 5))
ax[0].set_xlabel("$l$", fontsize=12)
ax[0].set_ylabel("$m$", fontsize=12)
ax[1].set_xlabel("$l$", fontsize=12)
ax[1].set_ylabel("$m$", fontsize=12)
ax[0].set_title(
    "$\max_{x \in (0,1)} |\\frac{d^2 Z_{lm}(x)}{dx^2} - \\frac{d^2 \\tilde{Z}_{lm}^{poly}(x)}{dx^2}|$",
    fontsize=14,
)
ax[1].set_title(
    "$\max_{x \in (0,1)} |\\frac{d^2 Z_{lm}(x)}{dx^2} - \\frac{d^2 \\tilde{Z}_{lm}^{jacobi}(x)}{dx^2}|$",
    fontsize=14,
);

../_images/notebooks_zernike_eval_20_0.png

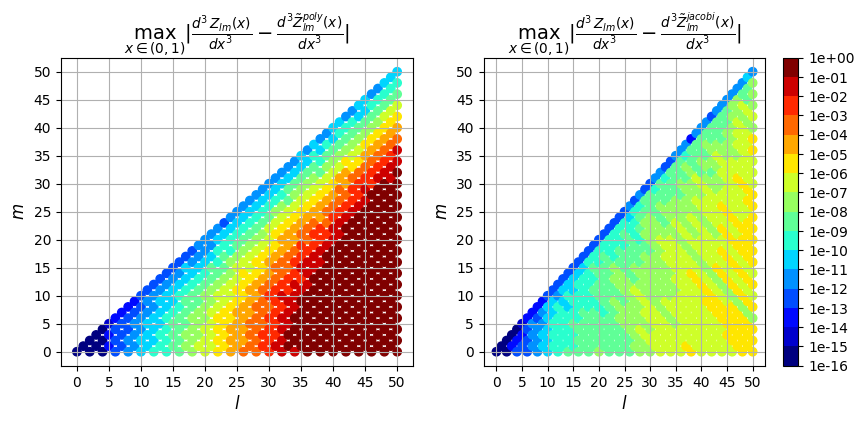
3rd derivative

[13]:

fig, ax = plt.subplots(1, 2, squeeze=True, figsize=(10, 4))
im = ax[0].scatter(
    basis.modes[:, 0],
    basis.modes[:, 1],
    c=np.max(abs(zp3 - zt3), axis=0),
    norm=norm,
    cmap=cmap,
)
im = ax[1].scatter(
    basis.modes[:, 0],
    basis.modes[:, 1],
    c=np.max(abs(zr3 - zt3), axis=0),
    norm=norm,
    cmap=cmap,
)
cbar = fig.colorbar(im, ticks=bounds)
cbar.ax.set_yticklabels(["{:.0e}".format(foo) for foo in bounds])
ax[0].grid(True)
ax[1].grid(True)
ax[0].set_xticks(np.arange(0, 55, 5))
ax[0].set_yticks(np.arange(0, 55, 5))
ax[1].set_xticks(np.arange(0, 55, 5))
ax[1].set_yticks(np.arange(0, 55, 5))
ax[0].set_xlabel("$l$", fontsize=12)
ax[0].set_ylabel("$m$", fontsize=12)
ax[1].set_xlabel("$l$", fontsize=12)
ax[1].set_ylabel("$m$", fontsize=12)
ax[0].set_title(
    "$\max_{x \in (0,1)} |\\frac{d^3 Z_{lm}(x)}{dx^3} - \\frac{d^3 \\tilde{Z}_{lm}^{poly}(x)}{dx^3}|$",
    fontsize=14,
)
ax[1].set_title(
    "$\max_{x \in (0,1)} |\\frac{d^3 Z_{lm}(x)}{dx^3} - \\frac{d^3 \\tilde{Z}_{lm}^{jacobi}(x)}{dx^3}|$",
    fontsize=14,
);

../_images/notebooks_zernike_eval_22_0.png

Relative Error

0th derivative

[14]:

fig, ax = plt.subplots(1, 2, squeeze=True, figsize=(10, 4))
im = ax[0].scatter(
    basis.modes[:, 0],
    basis.modes[:, 1],
    c=np.max(abs(zp0 - zt0), axis=0) / np.mean(abs(zt0)),
    norm=norm,
    cmap=cmap,
)
im = ax[1].scatter(
    basis.modes[:, 0],
    basis.modes[:, 1],
    c=np.max(abs(zr0 - zt0), axis=0) / np.mean(abs(zt0)),
    norm=norm,
    cmap=cmap,
)
cbar = fig.colorbar(im, ticks=bounds)
cbar.ax.set_yticklabels(["{:.0e}".format(foo) for foo in bounds])
ax[0].grid(True)
ax[1].grid(True)
ax[0].set_xticks(np.arange(0, 55, 5))
ax[0].set_yticks(np.arange(0, 55, 5))
ax[1].set_xticks(np.arange(0, 55, 5))
ax[1].set_yticks(np.arange(0, 55, 5))
ax[0].set_xlabel("$l$", fontsize=12)
ax[0].set_ylabel("$m$", fontsize=12)
ax[1].set_xlabel("$l$", fontsize=12)
ax[1].set_ylabel("$m$", fontsize=12)
ax[0].set_title(
    "$\max_{x \in (0,1)} |Z_{lm}(x) - \\tilde{Z}_{lm}^{poly}(x)| / |\\bar{Z}_{lm}|$",
    fontsize=14,
)
ax[1].set_title(
    "$\max_{x \in (0,1)} |Z_{lm}(x) - \\tilde{Z}_{lm}^{jacobi}(x)| / |\\bar{Z}_{lm}|$",
    fontsize=14,
);

../_images/notebooks_zernike_eval_24_0.png

1st derivative

[15]:

fig, ax = plt.subplots(1, 2, squeeze=True, figsize=(10, 4))
im = ax[0].scatter(
    basis.modes[:, 0],
    basis.modes[:, 1],
    c=np.max(abs(zp1 - zt1), axis=0) / np.mean(abs(zt1)),
    norm=norm,
    cmap=cmap,
)
im = ax[1].scatter(
    basis.modes[:, 0],
    basis.modes[:, 1],
    c=np.max(abs(zr1 - zt1), axis=0) / np.mean(abs(zt1)),
    norm=norm,
    cmap=cmap,
)
cbar = fig.colorbar(im, ticks=bounds)
cbar.ax.set_yticklabels(["{:.0e}".format(foo) for foo in bounds])
ax[0].grid(True)
ax[1].grid(True)
ax[0].set_xticks(np.arange(0, 55, 5))
ax[0].set_yticks(np.arange(0, 55, 5))
ax[1].set_xticks(np.arange(0, 55, 5))
ax[1].set_yticks(np.arange(0, 55, 5))
ax[0].set_xlabel("$l$", fontsize=12)
ax[0].set_ylabel("$m$", fontsize=12)
ax[1].set_xlabel("$l$", fontsize=12)
ax[1].set_ylabel("$m$", fontsize=12)
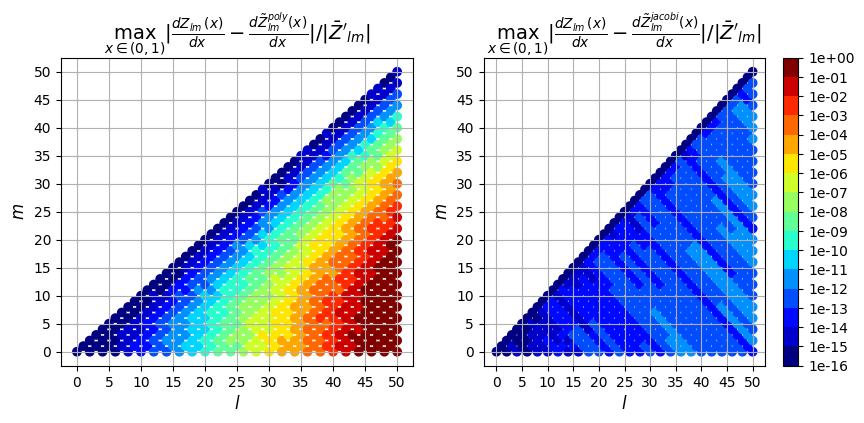
ax[0].set_title(
    "$\max_{x \in (0,1)} |\\frac{dZ_{lm}(x)}{dx} - \\frac{d\\tilde{Z}_{lm}^{poly}(x)}{dx}| / |\\bar{Z}'_{lm}|$",
    fontsize=14,
)
ax[1].set_title(
    "$\max_{x \in (0,1)} |\\frac{dZ_{lm}(x)}{dx} - \\frac{d\\tilde{Z}_{lm}^{jacobi}(x)}{dx}|/ |\\bar{Z}'_{lm}|$",
    fontsize=14,
);

../_images/notebooks_zernike_eval_26_0.png

2nd derivative

[16]:

fig, ax = plt.subplots(1, 2, squeeze=True, figsize=(10, 4))
im = ax[0].scatter(
    basis.modes[:, 0],
    basis.modes[:, 1],
    c=np.max(abs(zp2 - zt2), axis=0) / np.mean(abs(zt2)),
    norm=norm,
    cmap=cmap,
)
im = ax[1].scatter(
    basis.modes[:, 0],
    basis.modes[:, 1],
    c=np.max(abs(zr2 - zt2), axis=0) / np.mean(abs(zt2)),
    norm=norm,
    cmap=cmap,
)
cbar = fig.colorbar(im, ticks=bounds)
cbar.ax.set_yticklabels(["{:.0e}".format(foo) for foo in bounds])
ax[0].grid(True)
ax[1].grid(True)
ax[0].set_xticks(np.arange(0, 55, 5))
ax[0].set_yticks(np.arange(0, 55, 5))
ax[1].set_xticks(np.arange(0, 55, 5))
ax[1].set_yticks(np.arange(0, 55, 5))
ax[0].set_xlabel("$l$", fontsize=12)
ax[0].set_ylabel("$m$", fontsize=12)
ax[1].set_xlabel("$l$", fontsize=12)
ax[1].set_ylabel("$m$", fontsize=12)
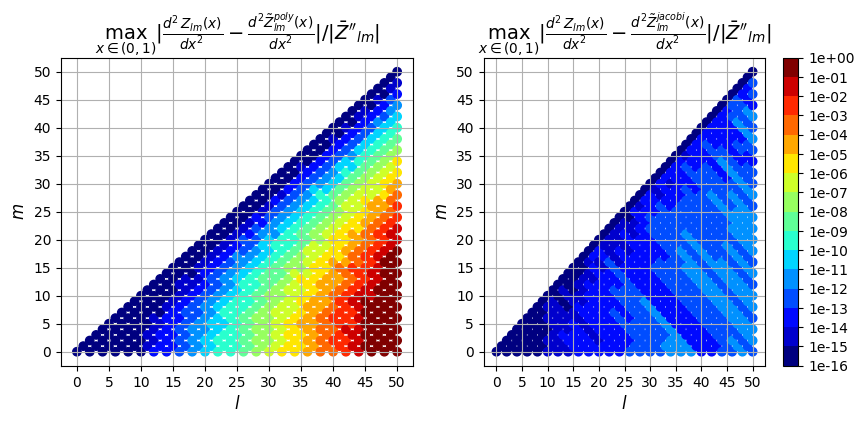
ax[0].set_title(
    "$\max_{x \in (0,1)} |\\frac{d^2Z_{lm}(x)}{dx^2} - \\frac{d^2\\tilde{Z}_{lm}^{poly}(x)}{dx^2}| / |\\bar{Z}''_{lm}|$",
    fontsize=14,
)
ax[1].set_title(
    "$\max_{x \in (0,1)} |\\frac{d^2Z_{lm}(x)}{dx^2} - \\frac{d^2\\tilde{Z}_{lm}^{jacobi}(x)}{dx^2}|/ |\\bar{Z}''_{lm}|$",
    fontsize=14,
);

../_images/notebooks_zernike_eval_28_0.png

3rd derivative

[17]:

fig, ax = plt.subplots(1, 2, squeeze=True, figsize=(10, 4))
im = ax[0].scatter(
    basis.modes[:, 0],
    basis.modes[:, 1],
    c=np.max(abs(zp3 - zt3), axis=0) / np.mean(abs(zt3)),
    norm=norm,
    cmap=cmap,
)
im = ax[1].scatter(
    basis.modes[:, 0],
    basis.modes[:, 1],
    c=np.max(abs(zr3 - zt3), axis=0) / np.mean(abs(zt3)),
    norm=norm,
    cmap=cmap,
)
cbar = fig.colorbar(im, ticks=bounds)
cbar.ax.set_yticklabels(["{:.0e}".format(foo) for foo in bounds])
ax[0].grid(True)
ax[1].grid(True)
ax[0].set_xticks(np.arange(0, 55, 5))
ax[0].set_yticks(np.arange(0, 55, 5))
ax[1].set_xticks(np.arange(0, 55, 5))
ax[1].set_yticks(np.arange(0, 55, 5))
ax[0].set_xlabel("$l$", fontsize=12)
ax[0].set_ylabel("$m$", fontsize=12)
ax[1].set_xlabel("$l$", fontsize=12)
ax[1].set_ylabel("$m$", fontsize=12)
ax[0].set_title(
    "$\max_{x \in (0,1)} |\\frac{d^3Z_{lm}(x)}{dx^3} - \\frac{d^3\\tilde{Z}_{lm}^{poly}(x)}{dx^3}| / |\\bar{Z}'''_{lm}|$",
    fontsize=14,
)
ax[1].set_title(
    "$\max_{x \in (0,1)} |\\frac{d^3Z_{lm}(x)}{dx^3} - \\frac{d^3\\tilde{Z}_{lm}^{jacobi}(x)}{dx^3}|/ |\\bar{Z}'''_{lm}|$",
    fontsize=14,
);

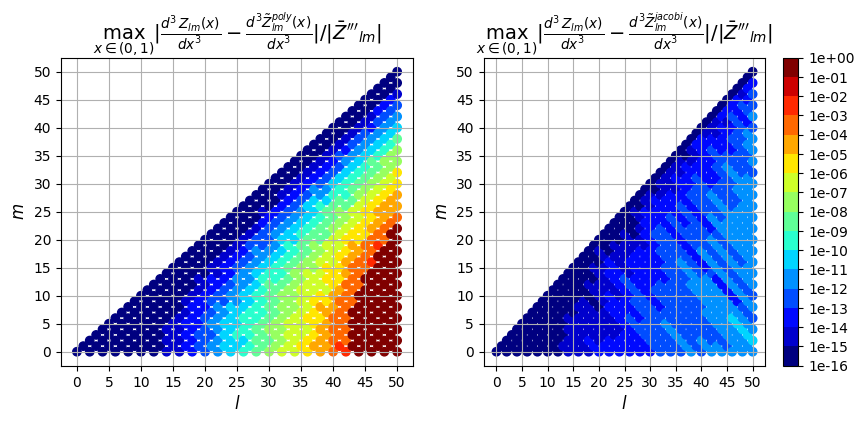
../_images/notebooks_zernike_eval_30_0.png

So in addition to being faster, the evaluation using the Jacobi recurrence relation is also significantly more accurate as the mode numbers increase, keeping absolute error less than \(10^{-5}\) and relative error less than \(10^{-9}\), while directly evaluating the polynomial leads to errors greater than 100% for large \(l\)